Теория хаоса
Введение в теорию хаоса
Что такое теория хаоса?
Теория хаоса это учение о постоянно изменяющихся сложных системах, основанное на математических концепциях, в форме ли рекурсивного процесса или набора дифференциальных уравнений, моделирующих физическую систему (реку́рсия — процесс повторения элементов самоподобным образом).Неправильные представления о теории хаоса
Широкая общественность обратила внимание на теорию хаоса благодаря таким фильмам, как "Парк юрского периода", и благодаря им же, постоянно увеличивается опасение теории хаоса со стороны общества. Однако, как и в отношении любой вещи, освещаемой средствами массовой информации, в отношении теории хаоса возникло много неправильных представлений.
Наиболее часто встречающееся несоответствие состоит в том, что люди полагают, что теория хаоса — это теория о беспорядке. Ничто не могло бы быть так далеко от истины! Это не опровержение детерминизма и не утверждение о том, что упорядоченные системы невозможны; это не отрицание экспериментальных подтверждений и не заявление о бесполезности сложных систем. Хаос в теории хаоса и есть порядок — и даже не просто порядок, а сущность порядка.Это правда, что теория хаоса утверждает, что небольшие изменения могут породить огромные последствия. Но одной из центральных концепций в теории является невозможность точного предсказания состояния системы. В общем, задача моделирования общего поведения системы вполне выполнима, даже проста. Таким образом, теория хаоса сосредотачивает усилия не на беспорядке системы — наследственной непредсказуемости системы — а на унаследованном ей порядке — общем в поведении похожих систем.
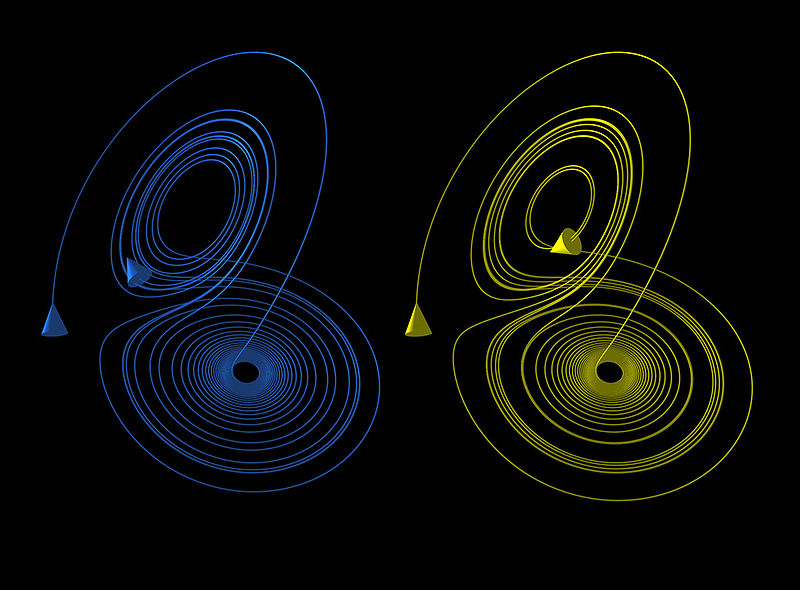
Таким образом, было бы неправильным сказать, что теория хаоса о беспорядке. Чтобы пояснить это на примере, возьмем аттрактор Лоренца. Он основан на трех дифференциальных уравнениях, трех константах и трех начальных условиях.
Теория хаоса о беспорядке
Аттрактор представляет поведение газа в любое заданное время, и его состояние в определенный момент зависит от его состояния в моменты времени, предшествовавшие данному. Если исходные данные изменить даже на очень маленькие величины, скажем, эти величины малы настолько, что соизмеримы с вкладом отдельных атомов в число Авогадро (что является очень маленьким числом по сравнению со значениями порядка 1024), проверка состояния аттрактора покажет абсолютно другие числа. Это происходит потому, что маленькие различия увеличиваются в результате рекурсии.
Однако, несмотря на это, график аттрактора будет выглядеть достаточно похоже. Обе системы будут иметь абсолютно разные значения в любой заданный момент времени, но график аттрактора останется тем же самым, т.к. он выражает общее поведение системы.
Теория хаоса говорит, что сложные нелинейные системы являются наследственно непредсказуемыми, но, в то же время, теория хаоса утверждает, что способ выражения таких непредсказуемых систем оказывается верным не в точных равенствах, а в представлениях поведения системы — в графиках странных аттракторов или во фракталах. Таким образом, теория хаоса, о которой многие думают как о непредсказуемости, оказывается, в то же время, наукой о предсказуемости даже в наиболее нестабильных системах.
Применение теории хаоса в реальном мире
При появлении новых теорий, все хотят узнать что же в них хорошего. Итак что хорошего в теории хаоса? Первое и самое важное — теория хаоса — это теория. А значит, что большая ее часть используется больше как научная основа, нежели как непосредственно применимое знание. Теория хаоса является очень хорошим средством взглянуть на события, происходящие в мире отлично от более традиционного четко детерминистического взгляда, который доминировал в науке со времен Ньютона. Зрители, которые посмотрели Парк Юрского периода, без сомнения боятся, что теория хаоса может очень сильно повлиять на человеческое восприятие мира, и, в действительности, теория хаоса полезна как средство интерпретации научных данных по-новому. Вместо традиционных X-Y графиков, ученые теперь могут интерпретировать фазово-пространственные диаграммы которые — вместо того, чтобы описывать точное положение какой-либо переменной в определенный момент времени — представляют общее поведение системы. Вместо того, чтобы смотреть на точные равенства, основанные на статистических данных, теперь мы можем взглянуть на динамические системы с поведением похожим по своей природе на статические данные — т.е. системы с похожими аттракторами. Теория хаоса обеспечивает прочный каркас для развития научных знаний.
Однако, согласно вышесказанному не следует, что теория хаоса не имеет приложений в реальной жизни.
Техники теории хаоса использовались для моделирования биологических систем, которые, бесспорно, являются одними из наиболее хаотических систем из всех что можно себе представить. Системы динамических равенств использовались для моделирования всего — от роста популяций и эпидемий до аритмических сердцебиений.
В действительности, почти любая хаотическая система может быть смоделирована — рынок ценных бумаг порождает кривые, которые можно легко анализировать при помощи странных аттракторов в отличие от точных соотношений; процесс падения капель из протекающего водопроводного крана кажется случайным при анализе невооруженным ухом, но если его изобразить как странный аттрактор, открывается сверхъестественный порядок, которого нельзя было бы ожидать от традиционных средств.
Фракталы находятся везде, наиболее заметны в графических программах как например очень успешная серия продуктов Fractal Design Painter. Техники фрактального сжатия данных все еще разрабатываются, но обещают удивительные результаты как например коэффициента сжатия 600:1. Индустрия специальных эффектов в кино, имела бы горазда менее реалистичные элементы ландшафта (облака, скалы и тени) без технологии фрактальной графики.
В физике фракталы естественным образом возникают при моделировании нелинейных процессов, таких, как турбулентное течение жидкости, сложные процессы диффузии-адсорбции, пламя, облака и т. п. Фракталы используются при моделировании пористых материалов, например, в нефтехимии. В биологии они применяются для моделирования популяций и для описания систем внутренних органов (система кровеносных сосудов).
И, конечно, теория хаоса дает людям удивительно интересный способ того, как приобрести интерес к математике, одной из наиболее мало-популярной области познания на сегодняшний день.